Batch 3 - Class 114 - Circles on a grid, Packing Sardines
Pre-Class Problem:
- Can you solve the above magic triangle for 9 digits instead of 6?
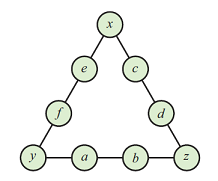
- Solution: There is one solution for each S value between 17 and 23, corresponding to C values between 6 and 24 - i.e there are 7 solution groups. Check if number of solutions for 1..12 could be 10 solution groups.
Attendance: Smiti, Muskaan, Anisha, Arushi, Tishyaa, Nandini, Aneyaa, Khushi, Anshi, Liza, Ishaan, Ahana, Kabir, Manya, Diya, Arnav, Zorawar
Class Notes:
Circles on a Grid
In this problem, we will look to find the minimum number of circles that can cover all points on a given grid.
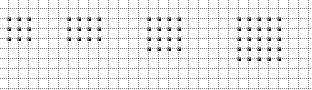
The earlier ones are relatively easy. Lets see if you can solve the last one.
- Instructor Notes: If kids are not able to get to it, drop a hint to check if its possible in 5 circles
- If there are 5 circles, how many points must a circle cover on an average?
- So if we want to start with circles that cover the maximum number of points, which ones would those be?
- Now walk down to successive circles
- Answer:
.png)
Spot the Pattern - Packing Square Sardines
Look at the following patterns and figure out a pattern on how squares are packed. To illustrate the pattern, draw the result if you pack a 16x16 square
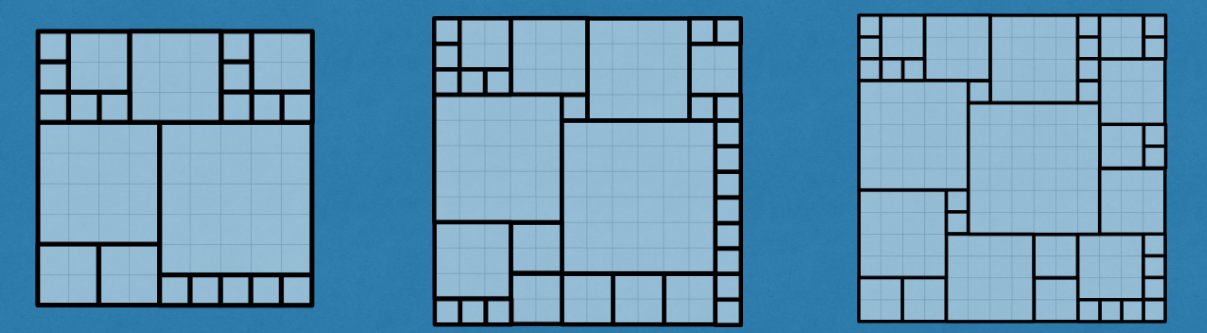
- If kids are not able to figure out, show them smaller samples
- What area is each kind of square taking?
- Can you get these to be as close as possible? What size of large square may permit that?
- Can you get these as far as possible?
Homework
Lets try another shape, and see if you can fit in those

- If you could choose the shapes, can you get area occupied by each shape equal?
References: